Research in music information retrieval has produced many possibilities for developing artificial intelligence (AI) algorithms that can perform a wide variety of musically-based tasks, including even music composition itself. The availability of vast musical datasets like the Million Song Dataset [Bertin et al. 2011] and Spotify's Web API has made it possible for researchers to acquire algorithmically-determined characteristics of a song's key, mode, pitch content, and more. At the same time, the existence of these large datasets has made it possible for researchers to take a 'big data'[1] approach to various styles of Western music. One notable example is the work by Serrà et al [Serrà et al. 2012b] which showed the changes and trends related to pitch transitions, the homogenization of the timbral palette and growing loudness levels that have shaped pop music over the past 60 years. The authors went on to suggest that past songs might be modernized into new hits by restricting pitch transitions, reducing timbral variety and making them louder. Tanya Clement further suggests how studying musical big data lends itself quite well to music related tasks, especially music composition, since the “notion of scholars ‘reading’ visualizations [(complete representation of the data)] relates to composers or musicians who read scores … [as] the musical score is an attempt to represent complex relationships … across time and space” [Clement 2013].

Big data can also be used to create labelled instances for training supervised learners like neural nets (which tend to be “data-thirsty”) and can be easily parsed by unsupervised learners to find patterns. This more recent ability to train music-related AI programs has largely been directed towards autonomously generating music in the same vein as whatever genre, style or composer that particular program has been trained on. A good example of this is “The Bach Doodle,” which can supply a melody with appropriate counter-melodies, accompaniment and chord changes in the style of Johann Sebastian Bach [Huang et al. 2019].

While the availability of approaches such as Spotify's has allowed for the development of AI algorithms in music, many previous research projects have struggled to find felicitous links between this music-related big data and music itself. In the past, a common method involving the use of Krumhansl-Kessler profiles [Krumhansl and Kessler 1982], vectors of pitch correlation to the major or minor modes, allowed for mode or key predictability in some limited capacity. While it showed promise when applied to music of specific genres, it suffered when applied to a wider scope of genres or styles. We offer methods to alter KK-profiles, and the manner in which they are employed during preprocessing, to aid autonomous mode and key predictors ability and accuracy without being genre-specific. Without the ability to connect the intermediate dots, the overall accuracy of these algorithms diminishes and their output suffers accordingly. Indeed, AI-based autonomous generation is rarely up to the standards of composers or musicians creating new music. This paper offers preliminary solutions to two existing problems for which AI is typically used, mode and key prediction. We show that by equipping our algorithms with more background in music theory we can significantly improve their accuracy. The more the program learns about the music theoretic principles of mode and key, the better it gets. Our more general argument is that one way to help bridge the gap between music-related big data and AI is to give algorithms a strong grounding in music theory.

For the purpose of this paper, we looked at only the two most common modes in Western Music, the major and minor modes. These are also the only modes analyzed by The Million Song Dataset and Spotify's Web API. The major and minor modes are a part of the “Diatonic Collection,” which refers to “any scale [or mode] where the octave is divided evenly into seven steps” [Laitz 2003]. A step can be either a whole or half step (whole tone or semitone) and the way that these are arranged in order to divide the octave will determine if the mode is major or minor. A major scale consists of the pattern W-W-H-W-W-W-H and the minor scale consists of W-H-W-W-H-W-W [Laitz 2003]. 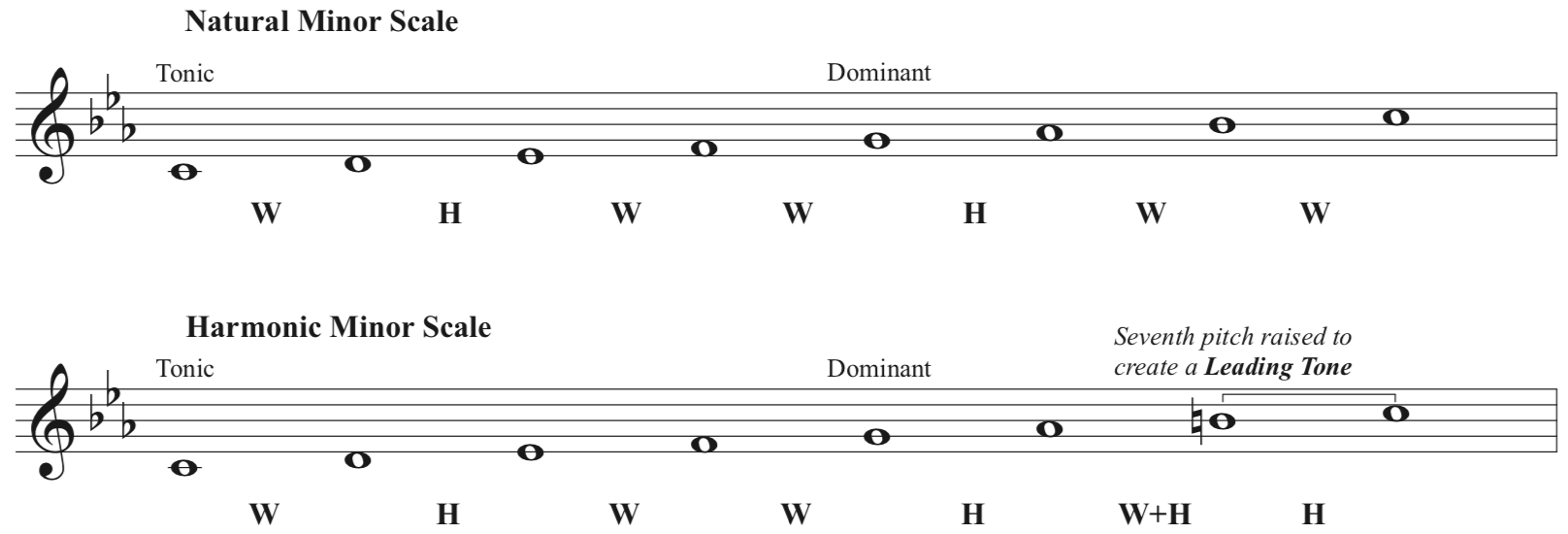Figure 1 shows a major scale starting on the pitch “C” and Figure 2 shows two types of minor scales starting on “C”. The seventh “step” in the harmonic minor scale example is raised in order to create a “leading tone.” The leading tone occurs when the seventh scale degree is a half step away from the first scale degree, also called the “tonic.” This leading tone to tonic relationship will become an important music theory principle that we use to train our AIs more accurately than previous published attempts.

Many previous papers which use supervised learning to determine mode or key test only against songs from specific genres or styles, and few make attempts at predicting mode regardless of genre. Even the often-cited yearly competition on musical key detection hosted by Music Information Retrieval Evaluation eXchange (MIREX) has participants' algorithms compete at classifying 1252 classical music pieces [İzmirli 2006] [Pauws 2004]. However, if we look again at Figure 1 and Figure 2, we can see that mode is not exclusive to genre or style, it is simply a specific arrangement of whole and half steps. So for a supervised learner programmed to “think” like a musician and thus determine mode based on its understanding of these music theory principles, genre or style should not affect the outcome. While this might work in a perfect world, artists have always looked for ways to “break away” from the norm and this can indeed manifest itself more in certain genres than others. Taking this into consideration, in this research we only selected songs for our separate ground truth set involving various genres which obey exact specifications for what constitutes as major or minor. This ground truth set will be a separate list of 100 songs labeled by us to further check the accuracy of our AI algorithms during testing. We wish to discuss shortcomings in the accuracy of past research that uses AI algorithms for predicting major or minor mode rather than to suggest a universal method for identifying all modes and scales.

This is one aspect where our research differs from previous papers. An AI system which incorporates a solid understanding of the rules of music theory pertaining to mode should be able to outperform others that do not incorporate such understanding or those that focus on specific genres. While certain genres or styles may increase the difficulty of algorithmically determining mode, the same is true for a human musical analyst. When successful, an AI algorithm for determining mode will process data much faster than a musician, who would either have to look through the score or figure it out by ear in order to make their decision. For parsing music-related big data quickly and accurately, speed is imperative. 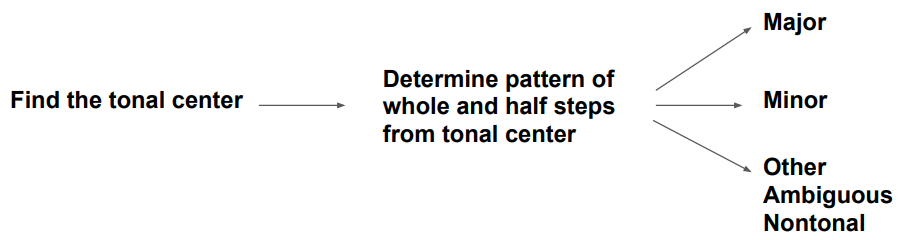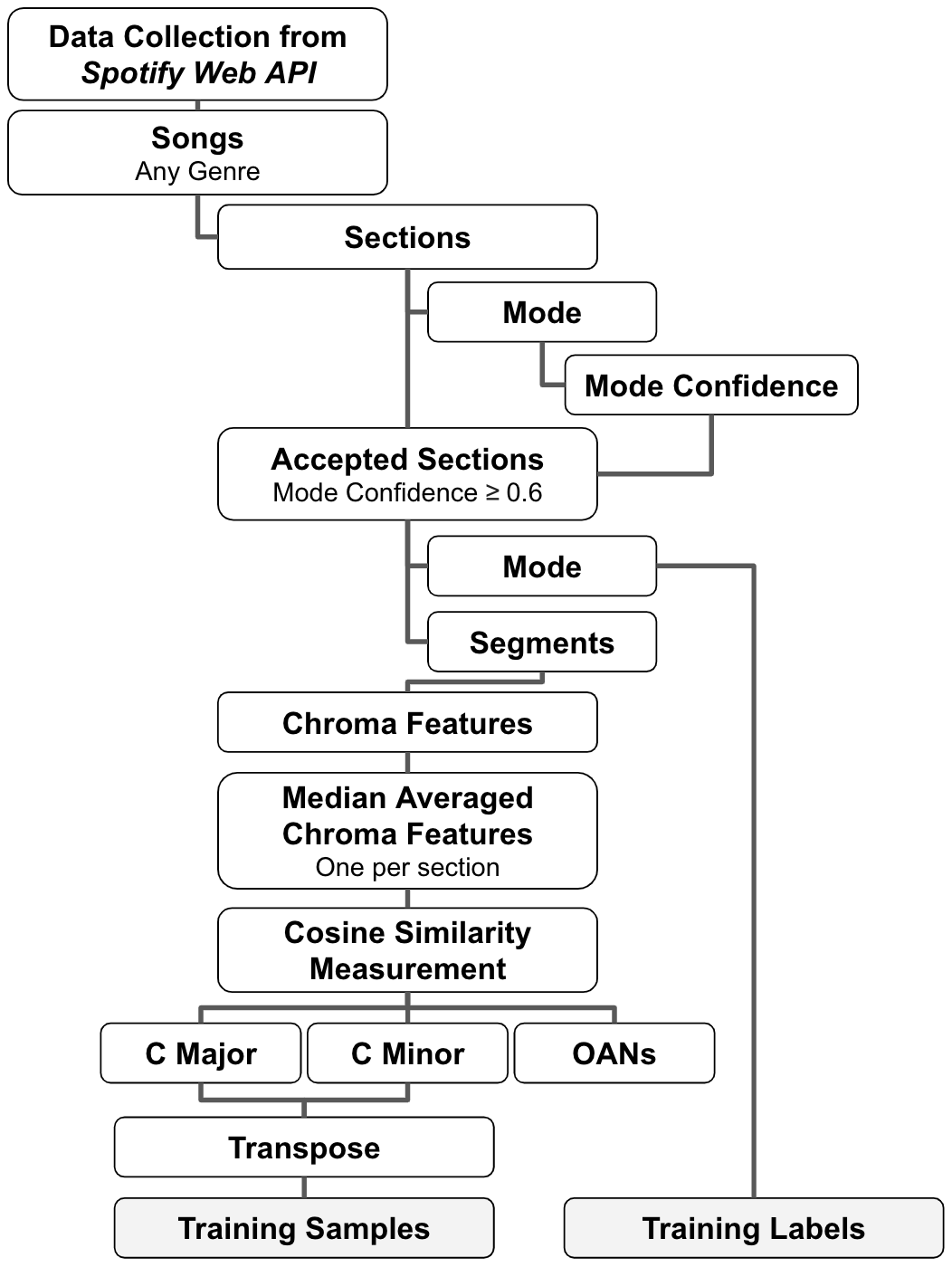Thus we suggest the following framework (Figure 3) by which a supervised learner can be trained to make predictions exclusively from pitch data in order to determine the mode of a song. The process is akin to methods used by human musical analysts. Below we also outline other areas where we apply a more musician-like approach to our methods to achieve greater accuracy.

As can be seen in Figure 3, any scale or mode that does not meet the exact specifications of major or minor we categorize as other, ambiguous or nontonal (OANs). The primary reason that past research has trained supervised learners on only one specific genre or style is to avoid OANs. When OANs are not segregated from major or minor modes, they are fit improperly, leading to misclassifications.

Other pertains to any scale separate from major or minor that still contains a tonal center. Some examples of this are: modes (except Ionian or Aeolian), whole tone scale, pentatonic scale, and non-Western scales. Nontonal refers to any song which does not center around a given pitch. A common occurrence of this can be found in various examples of “12-tone music,” where each pitch is given equal importance in the song and thus no tonic can be derived from it.

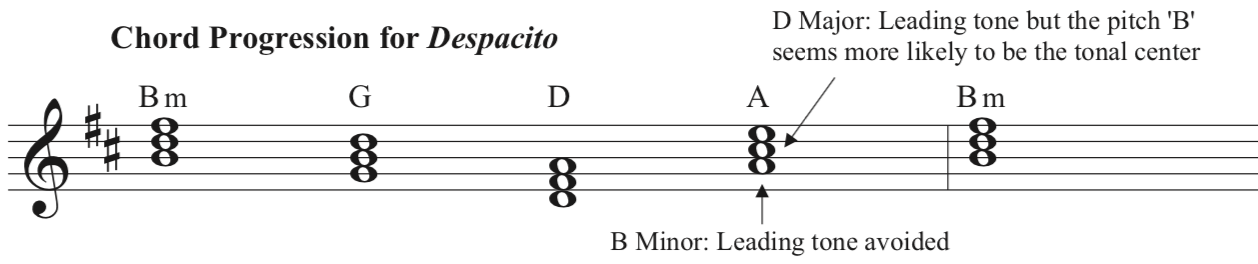
Where our paper differs from previous work is the handling of songs related to the outcome ambiguous. This occurs when either major or minor can be seen as an equally correct determination from the given pitches in a song. This most often occurs when chords containing the leading tone are avoided (Figure 4) and thus the remaining chords are consistent with both the major key and its relative minor (Figure 4 & Figure 5). The leading tone is a “tendency tone” or a tone that pulls towards a given target, in this case the tonic. This specific pull is one that can often signify a given mode and is therefore avoided in songs that the composer wished to float between the two modes. This can also be accomplished by simply using the relative minor's natural minor scale. Since the natural minor scale does not raise any pitches, it actually has the exact same notes (and resultant triads) as its relative major scale. Figure 6 gives an example of a well-known pop song Despacito [Fonsi and Yankee 2017] and given these rules, what mode can we say the song is in? This tough choice is a common occurrence, especially in modern pop music, which can explain why papers that focused heavily on dance music might have had accuracy issues.

Other authors have noted that their AI algorithms can mistake the major scale for its relative natural minor scale during prediction and it is likely that their algorithms did not account for the raised leading tone to truly distinguish major from minor. Since we focused on achieving higher accuracy than existing major vs minor mode prediction AI algorithms by incorporating music theory principles, we removed any instances of songs with an ambiguous mode from our ground truth set in order to get a clearer picture of how our system compares with the existing models. Adding other mode outcomes in order to detect OANs algorithmically is a part of our ongoing and future research.

The most popular method of turning pitch data into something that can be used to train machine learners comes in the form of “chroma features.” Chroma feature data is available for every song found in Spotify's giant database of songs through the use of their Web API. Chroma features are vectors containing 12 values (coded as real numbers between 0 and 1) reflecting the relative dominance of all 12 pitches over the course of a small segment, usually lasting no longer than a second [Jehan 2014]. Each vector begins on the pitch “C” and continues in chromatic order (C#, D, D#, etc.) until all 12 pitches are reached. In order to create an AI model that could make predictions on a wide variety of musical styles, we collected the chroma features for approximately 100,000 songs over the last 40 years. Spotify's Web API offers its data at different temporal resolutions, from the aforementioned short segments through sections of the work to the track as a whole.

Beyond chroma features, the API offers Spotify's own algorithmic analysis of musical features such as mode within these temporal units, and provides a corresponding level of confidence for each (coded as a real number between 0 and 1). We used Spotify's mode confidence levels to find every section within our 100,000 song list which had a mode confidence level of 0.6 or higher. The API's documentation states that “confidence indicates the reliability of its corresponding attribute... elements carrying a small confidence value should be considered speculative... there may not be sufficient data in the audio to compute the element with high certainty” [Jehan 2014] thus giving good reason to remove sections with lower confidence levels from the dataset. Previous work such as Serrà et al [Serrà et al. 2012b], Finley and Razi [Finley and Razi 2019] and Mahieu [Mahieu 2017] also used confidence thresholds, but at the temporal resolution of a whole track rather than the sections that we used. By analyzing at the level of sections, we were able to triple our training samples from 100,000 songs to approximately 350,000 sections. Not only did this method increase the number of potential training samples, but it allowed us to focus on specific areas of each song that were more likely to provide an accurate representation of each mode as they appeared. For example, a classical piece of music in “sonata form” will undergo a “development” section whereby it passes through contrasting keys and modes to build tension before its final resolve to the home key, mode and initial material. Pop music employs a similar tactic with “the bridge,” a section found after the midway point of a song to add contrast to the musical material found up until this point. Both of these contrasting sections might add confusion during the training process if the song is analyzed as a whole, but removing them or analyzing them separately gives the program more accurate training samples. The ability to gain more training samples from the original list of songs has the advantage of providing more data for training a supervised learner.

In previous work, a central tendency vector was created by taking the mean of each of the 12 components of the chroma vectors for a whole track, and this was then labelled as either major or minor for training. In an effort to mitigate the effects of noise on our averaged vector in any given recording, we found that using the medians rather than means gave us a better representation of the actual pitch content unaffected by potential outliers in the data. One common example is due to percussive instruments, such as a drum kit's cymbals, that happen to emphasize pitches that are “undesirable” for determining the song's particular key or mode. If that cymbal hit only occurs every few bars of music, but the “desirable” pitches occur much more often, we can lessen the effect that cymbal hit will have on our outcome by using a robust estimator. A musician working with a score or by ear would also filter out any unwanted sounds that did not help in mode determination. We found the medians of every segment's chroma feature vector found within each of our 350,000 sections.

The last step in the preparation process is to transpose each chroma vector such that they are all aligned into the same key. As our neural network (NN) will only output predictions of major or minor, we want to have the exact same tonal center for each chroma vector to easily compare between their whole and half step patterns (Figure 3). We based our transposition method on the one described by Serrà et al [Serrà et al. 2012b] and also used in their 2012 work. This method determines an “optimal transposition index” (OTI) by creating a new vector of the dot products between a chroma vector reflecting the key they wish to transpose to and the twelve possible rotations (i.e., 12 possible keys) of a second chroma vector. Using a right circular shift operation, the chroma vector is rotated by one half step each time until the maximum of 12 is reached. Argmax, a function which returns the position of the highest value in a vector, provides the OTI from the list of dot product correlation values, thus returning the number of steps needed to transpose the key of one chroma vector to match another (see Appendix 1.1 for a more detailed formula). Our method differs slightly from Serrà et al: since our vectors are all normalized, we used cosine similarity instead of the related dot product.

In order to train a neural network for mode prediction, some previous studies used the mode labels from the Spotify Web API for whole tracks or for sections of tracks. When we checked these measures against our own separate ground truth set (analyzed by Lupker), we discovered that the automated mode labeling was relatively inaccurate (Table 1). Instead we adapted the less complex method of Finley & Razi [Finley and Razi 2019], which reduced the need for training NNs. 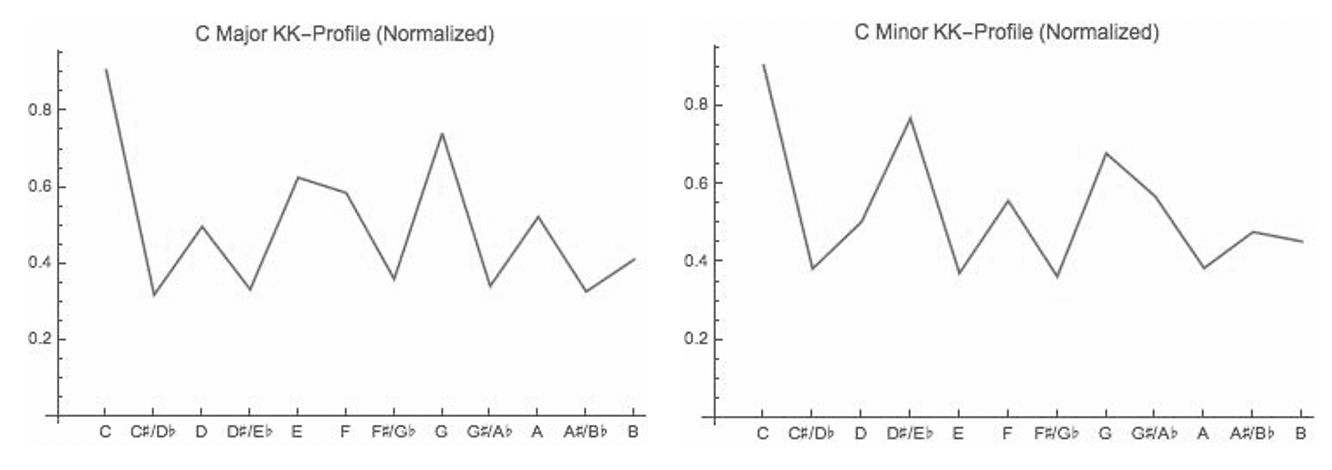They compared chroma vectors to “KK-Profiles” to distinguish mode and other musical elements. Krumhansl and Kessler profiles (Figure 7) come from a study where human subjects were asked to rate how well each of the twelve chromatic notes fit within a key after hearing musical elements such as scales, chords or cadences [Krumhansl and Kessler 1982]. The resulting vector can be normalized to the range between 0-1 for direct comparisons to chroma vectors using similarity measures. By incorporating both modified chroma transpositions and KK-profile similarity tests, we were able to label our training data in a novel way.

To combine these two approaches, we first rewrite Serrà et al's formula (Appendix 1.1) to incorporate Finley and Razi's method by making both KK-profile vectors (for major and minor modes) the new 'desired vectors' by which we will transpose our chroma vector set. This will eventually transpose our entire set of vectors to C major and C minor since the tonic of the KK-profiles is the first value in the vector, or pitch “C”. Correlations between KK-profiles and each of the 12 possible rotations of any given chroma vector are determined using cosine similarity. Instead of using the function which would return the position of the vector rotation that has the highest correlation (argmax), we use a different function which tells us what that correlation value is (amax). Two new lists are created. One is a list of the highest possible correlations for each transposed chroma vector and the major KK-profile, while the other is a list of correlations between each transposed chroma vector and the minor KK-profile. Finally, to determine the mode of each chroma vector, we then simply use a function to determine the position of the higher correlated value between these two lists, position 0 for major and 1 for minor (see Appendixes 1.2.1 & 1.2.2).

As noted by Finley & Razi, the most common issue affecting accuracy levels for supervised or unsupervised machine learners attempting to detect the mode or key is “being off by a perfect musical interval of a fifth from the true key, relative mode errors or parallel mode errors” [Finley and Razi 2019]. Unlike papers which followed the MIREX competition rules, our algorithm does not give partial credit to miscalculations no matter how closely related they may be to the true mode or key. Instead we offer methods to reduce these errors. To attempt to correct these issues for mode detection, it is necessary to address the potential differences between a result from music psychology, like the KK-profiles, and the music theoretic concepts that they quantify. As we mentioned earlier, the leading tone in a scale is one of the most important signifiers of mode. In the Despacito example, where the leading tone is avoided, it is hard to determine major or minor mode. In the (empirically determined) KK-profiles, the leading tone seems to be ranked comparatively low relative to the importance it holds theoretically. If the pitches are ordered from greatest to lowest perceived importance, the leading tone doesn't even register in the top five in either KK-profile. This might be a consequence of the study design, which asked subjects to judge how well each note seemed to fit after hearing other musical elements played.

The distance from the tonic to the leading tone is a major seventh interval (11 semitones). Different intervals fall into groups known as consonant or dissonant. Laitz defines consonant intervals as “stable intervals… such as the unison, the third, the fifth (perfect only)” and dissonant intervals as “unstable intervals… [including] the second, the seventh, and all diminished and augmented intervals” [Laitz 2003]. More dissonant intervals are perceived as having more tension. Rather than separating intervals into categories of consonant and dissonant, Hindemith ranks them on a spectrum, which represents their properties more effectively. He ranks the octave as the “most perfect,” the major seventh as the “least perfect” and all intervals in between as “decreasing in euphony in proportion to their distance from the octave and their proximity to the major seventh” [Hindemith 1984]. While determining the best method of interval ranking is irrelevant to this paper, both theorists identify the major seventh as one of the most dissonant intervals. Thus, if the leading tone were to be played by itself (that is, without the context of a chord after a musical sequence) it might sound off, unstable or tense due to the dissonance of a major seventh interval in relation to the tonic. In a song's chord progression or melody, this note will often be given context by its chordal accompaniment or the note might be resolved by subsequent notes. These methods and others will 'handle the dissonance' and make the leading tone sound less out of place. We concluded that the leading tone value found within the empirical KK-profiles should be boosted to reflect its importance in a chord progression in the major or minor mode. Our tests showed that boosting the original major KK-profile's 12th value from 2.88 to 3.7 and the original minor KK-profile's 12th value from 3.17 to 4.1 increased the accuracy of the model at determining the correct mode by removing all instances where misclassifications were made between relative major and minor keys.

Our training samples include a list of mode determinations labelling our 350,000 chroma vectors. However, the algorithm assumes that every vector is in a major or minor mode with no consideration for OANs. Trying to categorize every vector as either major or minor leads to highly inaccurate results during testing, and seems to be a main cause of miscalculations made by the mode prediction algorithms of Spotify's Web API and the Million Song Dataset. To account for other or nontonal scales, we can set a threshold of acceptable correlation values (major and minor modes) and unacceptable values (other or nontonal scales). Our testing showed that a threshold of greater than or equal to 0.9 gave the best accuracy on our ground truth set for determining major or minor modes. These unacceptable vectors contain other or nontonal scales and future research will determine ways of addressing and classifying these further.

To address ambiguous mode determinations between relative major and minor modes, we can set another threshold for removing potentially misleading data for training samples. While observing the correlation values used to determine major or minor labels, we set a further constraint when these values are too close to pick between them confidently. If the absolute difference between the two values is less than or equal to 0.02, we determine these correlation values to be indistinguishable and thus likely to reflect an ambiguous mode. As mentioned earlier, this is likely due to the song's chord progression avoiding certain mode determining factors such as the leading tone, and therefore the song can fit almost evenly into either the major or minor classification.

After filtering out samples determined to be OANs, our sample size was reduced to approximately 100,000. From this dataset, 75% of the samples were selected to train the model and an even split of the remaining 25% of samples being withheld for testing and cross-validation to check the model's accuracy and performance. On the withheld test set, our model returned a very high accuracy of 99% during testing. We found that this was much better than the results reported from other studies on withheld test sets. This level of accuracy and the ability to compute the data quickly make it useful for parsing big data for any research that makes comparisons based on modes.

In addition to testing using only samples withheld from our large dataset, we created a separate ground truth set of 100 songs taken from various “top 100” charts from different genres such as pop, country, classical and jazz. This ground truth set was labeled ourselves by looking at the score of each song and comparing it with the exact recording found on Spotify (in order to make sure it wasn't a version recorded in a different key). Our NN reached an accuracy of 88% on the outside ground truth set. The discrepancy is perhaps due to learning from samples that were improperly labelled during cosine similarity measures against KK-profiles. Since this model only outputs major or minor, it is hard to track the exact details of each misclassification. It could be miscalculating a result based on relative major or minors, parallel major or minors (C major vs C Minor) or just be completely off. These incorrectly identified modes will be further addressed in the next section where key is also determined, giving us a clearer understanding of the problem. It is important to note the very low accuracy of 18% in modes determined by Spotify's Web API. Future research based on the API's mode labelling algorithms should be tested against ground truth datasets before being used to make musicological claims.

With a highly accurate working model for mode detection, adding the ability to predict key becomes fairly straightforward. Our mode detection algorithm is based on the music theory principle of determining mode by first finding the tonic, then calculating the subsequent intervals. Additionally, this method assumes the tonic to be the most frequent note and therefore the tonic should always register as the most prominent note in any given median-averaged chroma vector. Thus when transposing each chroma vector in our ground truth set to C major or C minor, we must keep track of the initial position of the most prominent pitches, as these are our key determining features. This method of analyzing songs based on a non key-specific approach first, and then adding key labels afterwards is derived from the method of 'roman numeral analysis' in musicology. This kind of analysis is used by music theorists to outline triadic chord progressions found within tonal music [Laitz 2003]. In this method, uppercase numerals are used for major triads and lowercase numerals are used for minor triads (Figure 8). The method itself is not key-specific (besides a brief mention at the beginning), allowing the analysis of underlying chord relationships across multiple songs regardless of key. Considering that machine learning programs typically need large datasets for training, and that it is unlikely even large datasets will contain songs in every possible key in the same proportions, roman numeral analysis is ideal.

As our key predictions result from a simple labelling of our mode prediction neural network's output, we cannot compute accuracy of training. Past testing did include a second NN where the dataset taken from the mode detection NN was rotated to each of the 12 possible keys and then trained on that with 24 outputs for each major and minor key. This training resulted in 93% accuracy but we didn't find any significant increase over the method of applying labels after running the mode NN when testing against the ground truth set, therefore we decided against training a second NN to detect key as it saves training time. With the key labels added to the output of our mode NN, our model returned an accuracy level of 48%. While not nearly as accurate as our mode prediction algorithm, it is much higher than the Spotify Web API which returns an accuracy of 2% on our ground truth set.

It is also difficult to compare our accuracy on a ground truth set with any paper which used the MIREX competition dataset. MIREX's dataset contains remakes of real songs using Musical Instrument Digital Interface (MIDI) synthesizers which can be recorded straight into a computer, without the need for microphones. Furthermore, it is unclear if this dataset recreates the percussion synthetically for each song or if this is removed to allow easier access to the harmonic content for contestants to test their AI systems. As our training and testing uses actual recorded music and no MIDI representations there is a higher likelihood of noise or percussive elements to throw off our algorithm during testing the outside ground truth set. As of this research, we have not entered the MIREX competition, and thus do not have access to their datasets and cannot compare the performance of our algorithm with those which did. In future research we plan to enter the 2020 MIREX key detection competition and to draw more accurate comparisons with other key detection AI models.

Our much lower accuracy levels for key prediction in comparison to mode prediction are consistent with misclassification noted within previous research. While we were able to almost entirely remove instances of relative major and minor mode misclassifications, the big outstanding problem are keys classified by an interval of a fifth away. We see this as a potential limitation to the ability of supervised or unsupervised learning techniques to predict key (and mode to an almost perfect degree) from pitch content alone. If we imagine this method of determining mode and key from pitch content was performed by a human musician, the equivalent would be that of writing down each pitch in the first section (or the entirety) of a song and making predictions based on a tally. Since this method relies on the tonic being the most prominent pitch in this tally, the model will likely always fail when this is not the case. For example, a song might be in C major with a melody often repeating the pitch 'G' throughout the verse even while a tonic C major chord provides the accompaniment underneath. Since the pitch 'G' is found in the tonic chord of C major (Figure 4), it will sound good and be a theoretically correct decision. The repeated “G”, however, will be the most prominent note in the chroma vector section. The scale found a fifth away from a C major scale, G Major, shares all the same notes except one, thus confusing the model. Even with all the processes aimed at removing cases of OANs, a melody focused around the fifth interval of a tonic chord will constantly skew the data and the model will make miscalculations on key.

Our neural net model itself is quite simple and does not represent a novel approach to music AI models. Our research was instead focused on data preparation methods grounded in music theory helping to boost the accuracy of existing models by finding more appropriate links between music-related big data and the resultant outputs. Using our methods such as boosting the leading tone's prominence in the KK-profile and filtering out OANs, we were able to construct a model with a higher accuracy for mode prediction during both testing on a withheld subset of our dataset and on the external ground truth set labeled by Lupker. Our key prediction showed comparable results to previous research on a separate ground truth set and we see this as a limit to the ability of predicting key using a pitch-based tally classifier. The model's prediction can be too easily skewed by any song with a melody focused on the fifth interval of the tonic chord, mistaking the key for one a fifth away. Accessing the MIREX dataset would give us a better comparison with those papers which have competed in past competitions, but we predict similar results to those found in this paper.

Further steps we could take with this research would be to identify and label OANs to create a more universal mode and key prediction NN. The similarity measures specified in this paper could be repeated given chroma vector profiles of other modes and scales to compare against. This would be useful for any research projects experimenting with big data related to non-Western music. Another area for further research would be to apply our music theory based processes to some existing chord retrieval algorithms. Our testing leads us to believe that training NNs on chord transition networks as related to mode or key is the only way to reach accuracy levels comparable to human predictions. When musicians are faced with determining mode or key of a song with less obvious features, the last resort method is to look at the chord progression and make a decision based on that. Our predictions are that a learner trained to look for mode or key determining features of a chord progression will outperform those based on averaging tally counts of pitch.